Chapter 5 Interval comparison: Multi-path exploration results

Here we present the results for the best performances and activation gene coverage generated by each selection scheme replicate on the multi-path exploration diagnostic. Best performance found refers to the largest average trait score found in a given population. Note that activation gene coverage values are gathered at the population-level. Activation gene coverage refers to the count of unique activation genes in a given population; this gives us a range of integers between 0 and 100.

5.1 Analysis dependencies

library(ggplot2)
library(cowplot)
library(dplyr)
library(PupillometryR)

5.2 Data

base   = filter(base_over_time,   Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')
mi50   = filter(mi50_over_time,   Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')
mi5000 = filter(mi5000_over_time, Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')

base$Interval = '500'
mi50$Interval = '50'
mi5000$Interval = '5000'

df_ot = rbind(base, mi50, mi5000)
df_ot$Interval = factor(df_ot$Interval, levels=c('50','500','5000'))

base = filter(base_best,     Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')
mi50 = filter(mi50_best,     Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')
mi5000 = filter(mi5000_best, Diagnostic == 'MULTIPATH_EXPLORATION' & Structure == 'IS')

base$Interval = '500'
mi50$Interval = '50'
mi5000$Interval = '5000'

df_best = rbind(mi50,base,mi5000)
df_best$Interval = factor(df_best$Interval, levels = c('50','500','5000'))

5.3 Truncation selection

Here we analyze how the different population structures affect truncation selection (size 8) on the contradictory objectives diagnostic.

5.3.1 Performance

5.3.1.1 Performance over time

lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_fit_max) / DIMENSIONALITY,
    mean = mean(pop_fit_max) / DIMENSIONALITY,
    max = max(pop_fit_max) / DIMENSIONALITY
  )
ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 2.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle("Performance over time") +
  p_theme

5.3.1.2 Best performance

Best performancefound throughout the 50,000 generations.

filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & VAR == 'pop_fit_max') %>%
  ggplot(., aes(x = Interval, y = VAL / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Best performance')+
  p_theme + coord_flip()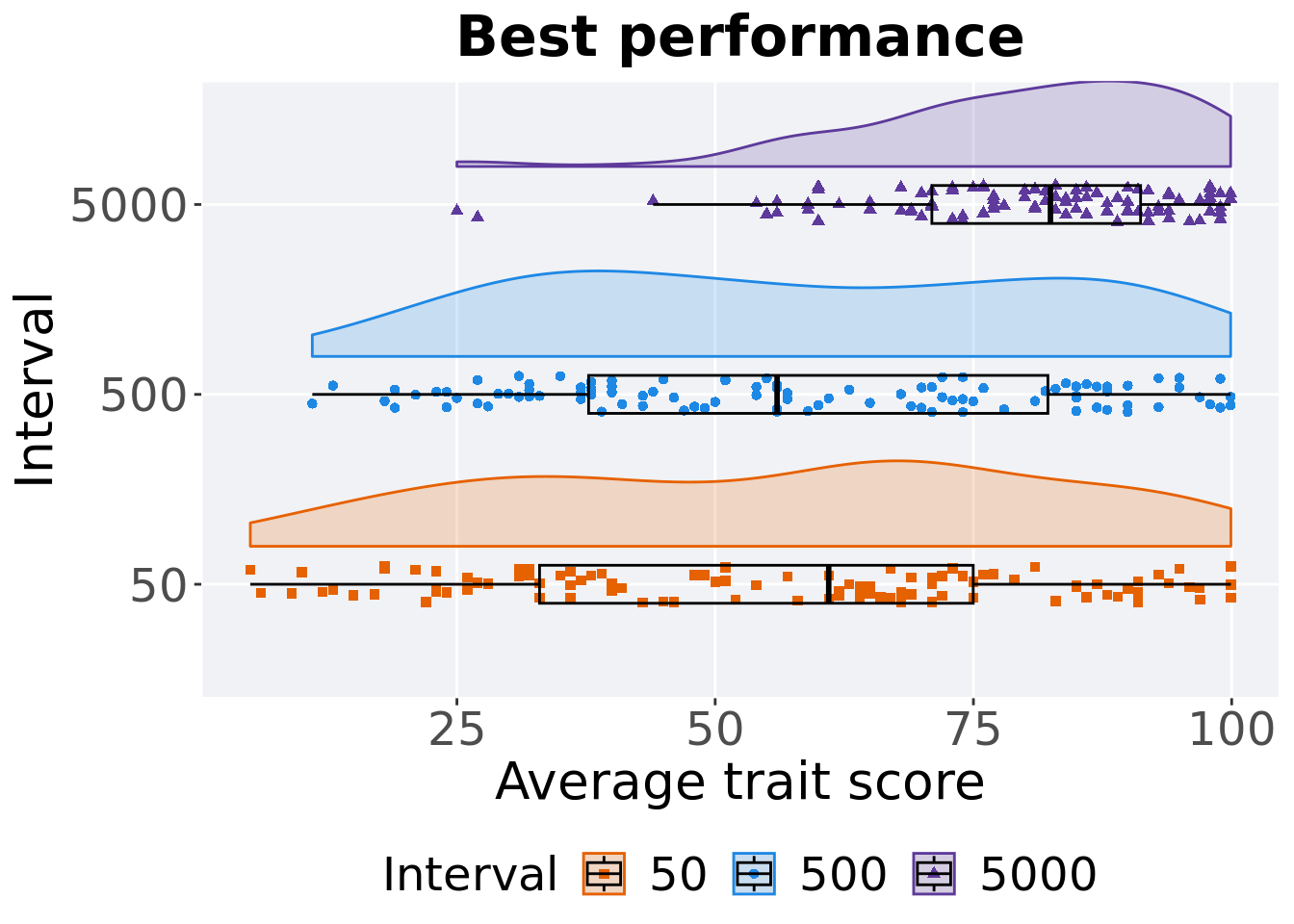

5.3.1.2.1 Stats

Summary statistics for the first generation a best performance found.

performance = filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & VAR == 'pop_fit_max')
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(VAL)),
    min = min(VAL, na.rm = TRUE) / DIMENSIONALITY,
    median = median(VAL, na.rm = TRUE) / DIMENSIONALITY,
    mean = mean(VAL, na.rm = TRUE) / DIMENSIONALITY,
    max = max(VAL, na.rm = TRUE) / DIMENSIONALITY,
    IQR = IQR(VAL, na.rm = TRUE) / DIMENSIONALITY
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0   5     61.0  55.6  99.9  42.0
## 2 500        100      0  11     56.0  58.3  99.9  44.5
## 3 5000       100      0  25.0   82.5  79.7  99.9  20.2

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(VAL ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  VAL by Interval
## Kruskal-Wallis chi-squared = 51.085, df = 2, p-value = 8.073e-12

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$VAL, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'g')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$VAL and performance$Interval 
## 
##      50      500    
## 500  0.87    -      
## 5000 1.9e-10 5.5e-09
## 
## P value adjustment method: bonferroni

5.3.1.3 Final performance

Best performance is found throughout in final generation.

filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_fit_max / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final performance')+
  p_theme + coord_flip()

5.3.1.3.1 Stats

Summary statistics for the best performance is found in final generation.

performance = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & Generations == 50000)
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_fit_max)),
    min = min(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    median = median(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    mean = mean(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    max = max(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    IQR = IQR(pop_fit_max / DIMENSIONALITY, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0   5     61.0  55.6  99.9  42.0
## 2 500        100      0  11     56.0  58.3  99.9  44.5
## 3 5000       100      0  25.0   82.5  79.7  99.9  20.2

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(pop_fit_max ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_fit_max by Interval
## Kruskal-Wallis chi-squared = 51.085, df = 2, p-value = 8.073e-12

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$pop_fit_max, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'g')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$pop_fit_max and performance$Interval 
## 
##      50      500    
## 500  0.87    -      
## 5000 1.9e-10 5.5e-09
## 
## P value adjustment method: bonferroni

5.3.2 Activation gene coverage

Activation gene coverage analysis.

5.3.2.1 Coverage over time

Activation gene coverage over time.

# data for lines and shading on plots
lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_act_cov),
    mean = mean(pop_act_cov),
    max = max(pop_act_cov)
  )

## `summarise()` has grouped output by 'Interval'. You can override using the
## `.groups` argument.

ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 1.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Activation gene coverage over time')+
  p_theme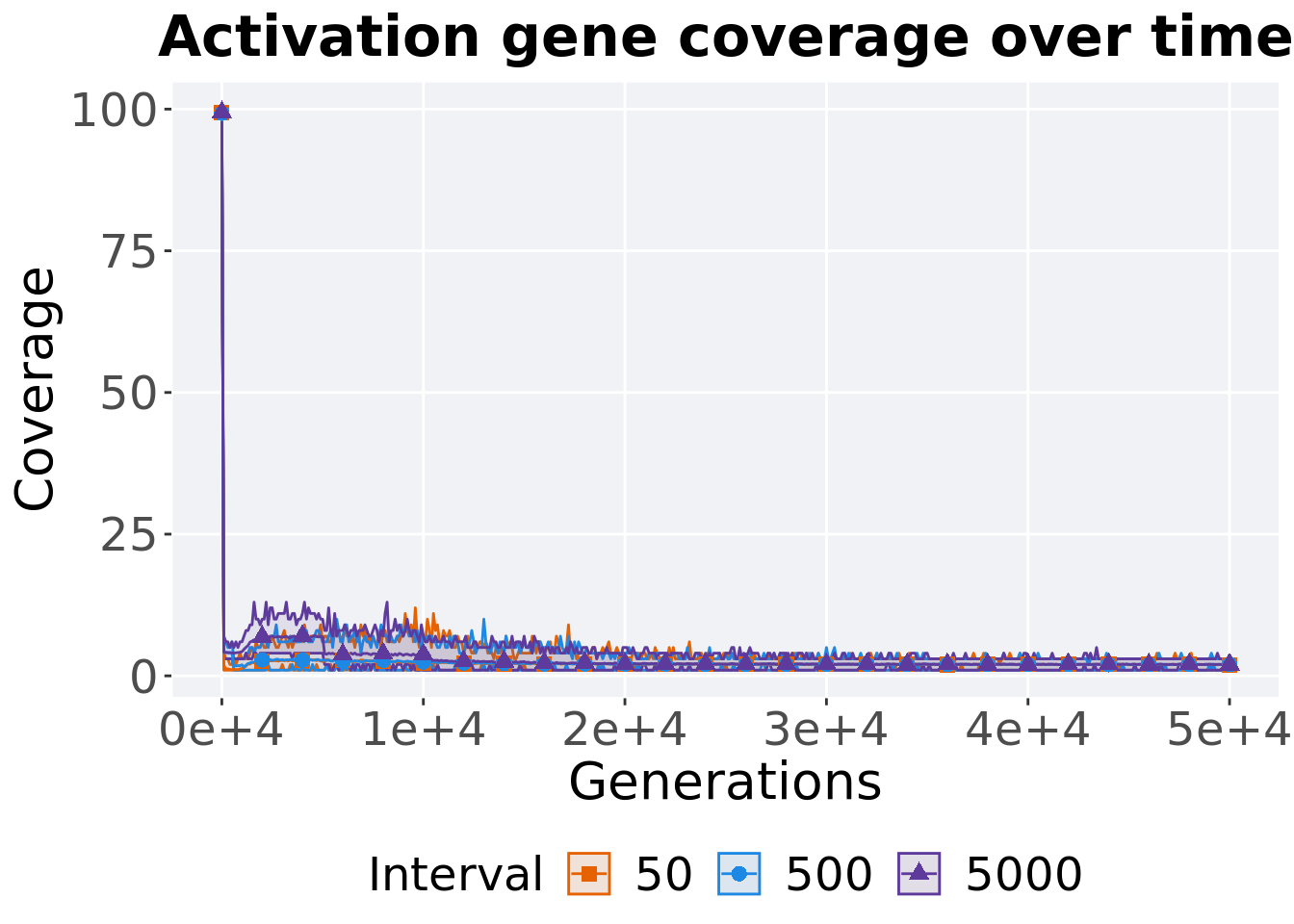

5.3.2.2 End of 50,000 generations

Activation gene coverage in the population at the end of 50,000 generations.

### end of run
filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_act_cov, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.3) +
  geom_point(position = position_jitter(height = .05, width = .05), size = 1.5, alpha = 0.5) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_shape_manual(values=SHAPE)+
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_discrete(
    name="Interval"
  ) +
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final activation gene coverage')+
  p_theme + coord_flip()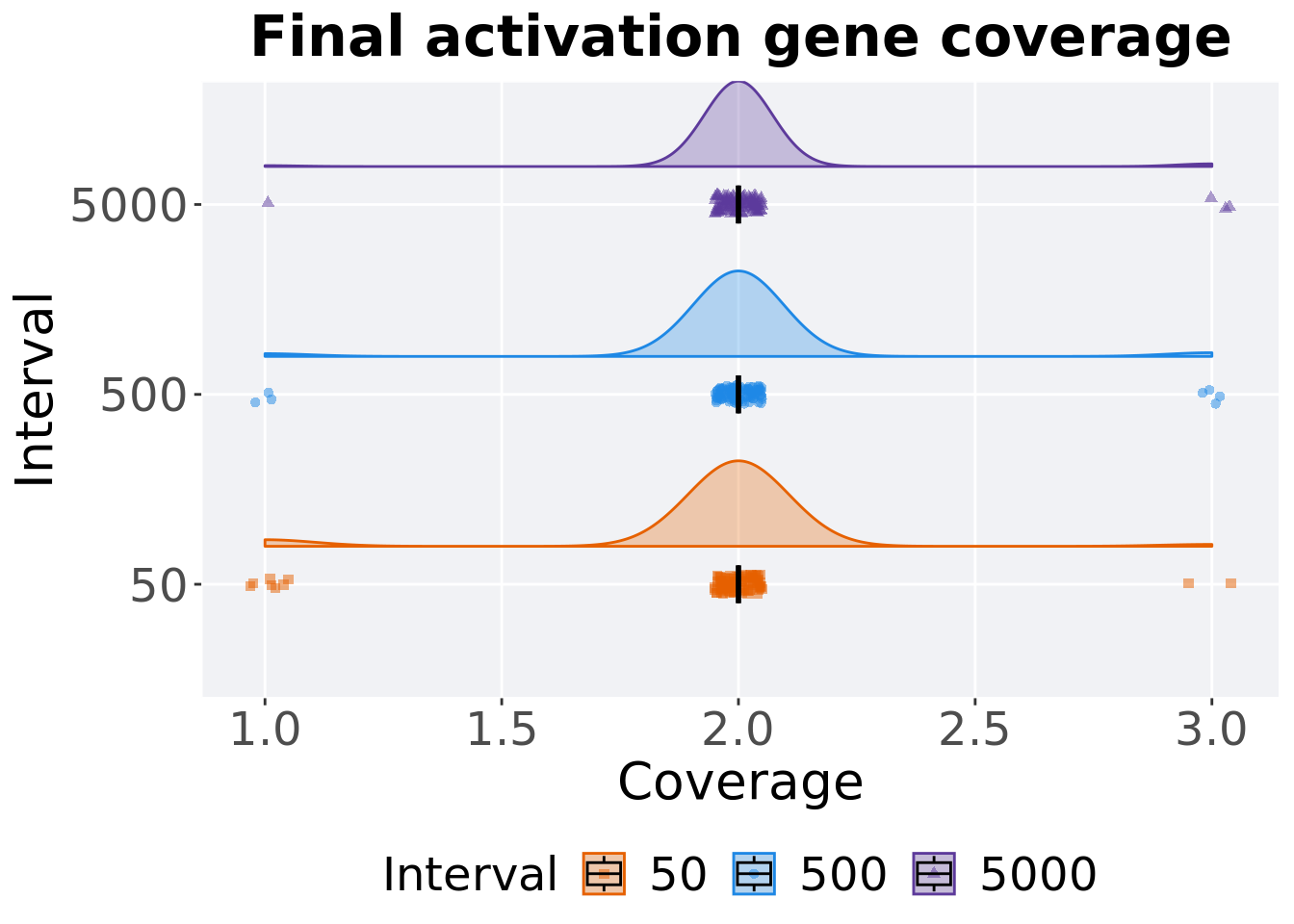

5.3.2.2.1 Stats

Summary statistics for activation gene coverage.

coverage = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TRUNCATION' & Generations == 50000)
coverage %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_act_cov)),
    min = min(pop_act_cov, na.rm = TRUE),
    median = median(pop_act_cov, na.rm = TRUE),
    mean = mean(pop_act_cov, na.rm = TRUE),
    max = max(pop_act_cov, na.rm = TRUE),
    IQR = IQR(pop_act_cov, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <int>  <dbl> <dbl> <int> <dbl>
## 1 50         100      0     1      2  1.95     3     0
## 2 500        100      0     1      2  2.01     3     0
## 3 5000       100      0     1      2  2.02     3     0

Kruskal–Wallis test provides evidence of no difference among activation gene coverage.

kruskal.test(pop_act_cov ~ Interval, data = coverage)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_act_cov by Interval
## Kruskal-Wallis chi-squared = 4.3029, df = 2, p-value = 0.1163

5.4 Tournament selection

Here we analyze how the different population structures affect tournament selection (size 8) on the contradictory objectives diagnostic.

5.4.1 Performance

5.4.1.1 Performance over time

lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_fit_max) / DIMENSIONALITY,
    mean = mean(pop_fit_max) / DIMENSIONALITY,
    max = max(pop_fit_max) / DIMENSIONALITY
  )
ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 2.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle("Performance over time") +
  p_theme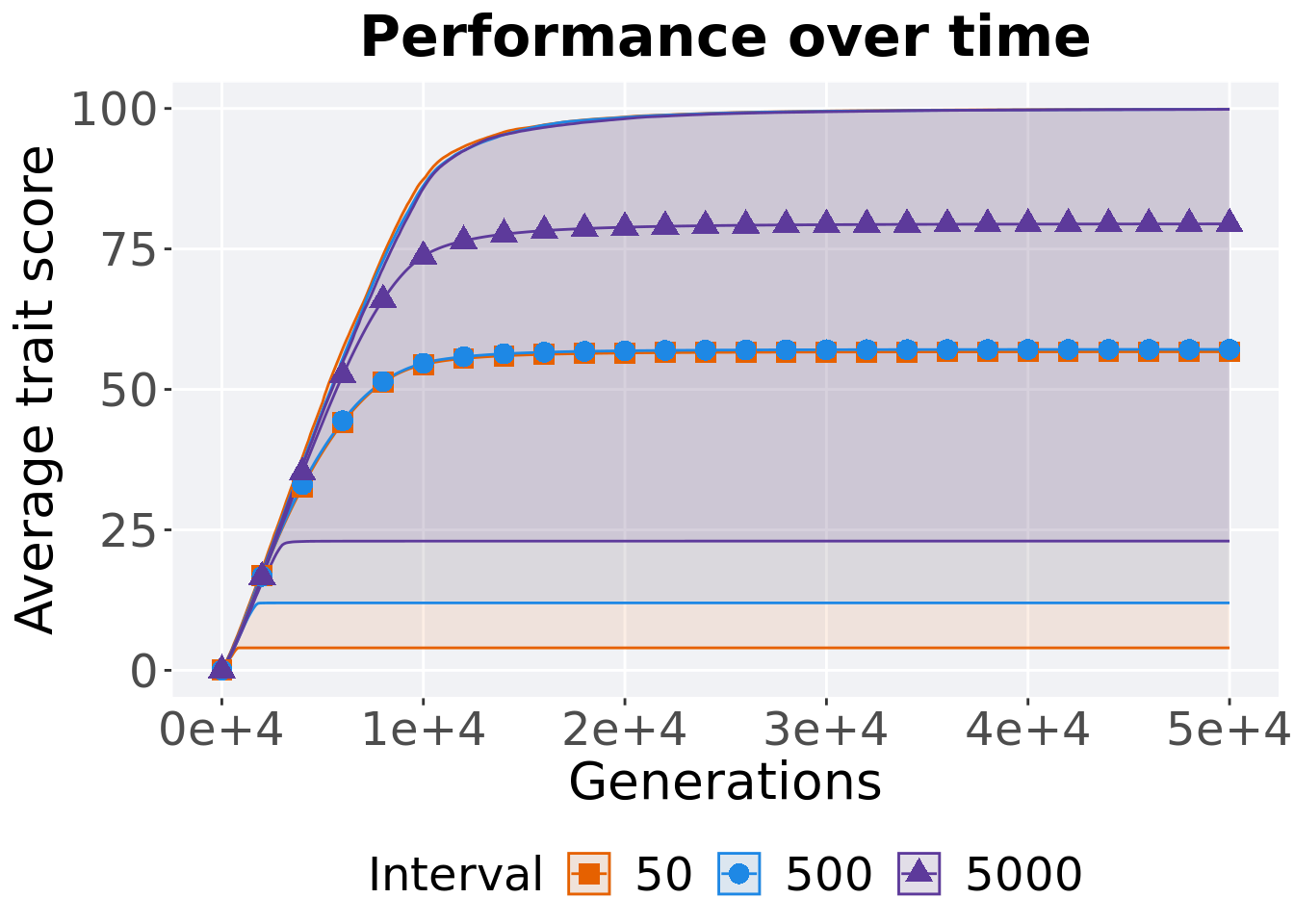

5.4.1.2 Best performance

Best performance is found throughout the 50,000 generations.

filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & VAR == 'pop_fit_max') %>%
  ggplot(., aes(x = Interval, y = VAL / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Best performance')+
  p_theme + coord_flip()

5.4.1.2.1 Stats

Summary statistics for the best performance found.

performance = filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & VAR == 'pop_fit_max')
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(VAL)),
    min = min(VAL, na.rm = TRUE) / DIMENSIONALITY,
    median = median(VAL, na.rm = TRUE) / DIMENSIONALITY,
    mean = mean(VAL, na.rm = TRUE) / DIMENSIONALITY,
    max = max(VAL, na.rm = TRUE) / DIMENSIONALITY,
    IQR = IQR(VAL, na.rm = TRUE) / DIMENSIONALITY
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0   4     58.5  56.7  99.9  45.5
## 2 500        100      0  12     59.0  57.1  99.9  43.5
## 3 5000       100      0  23.0   82.9  79.5  99.8  23.2

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(VAL ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  VAL by Interval
## Kruskal-Wallis chi-squared = 50.052, df = 2, p-value = 1.353e-11

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$VAL, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'g')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$VAL and performance$Interval 
## 
##      50      500    
## 500  1       -      
## 5000 2.6e-09 7.4e-10
## 
## P value adjustment method: bonferroni

5.4.1.3 Final performance

Best performance is found in final generation.

filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_fit_max / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final performance')+
  p_theme + coord_flip()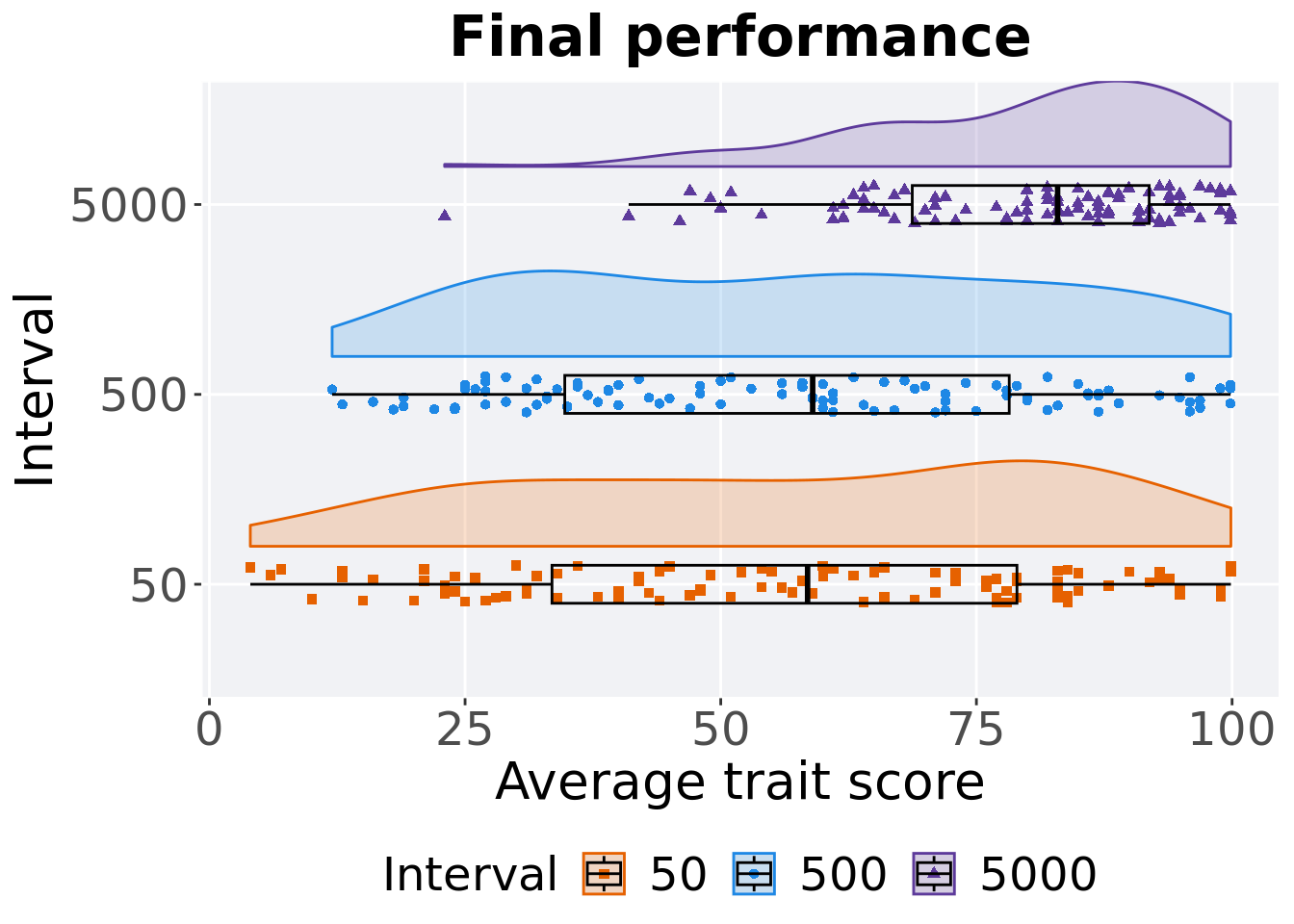

5.4.1.3.1 Stats

Summary statistics for best performance is found in final generation.

performance = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & Generations == 50000)
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_fit_max)),
    min = min(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    median = median(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    mean = mean(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    max = max(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    IQR = IQR(pop_fit_max / DIMENSIONALITY, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0   4     58.5  56.7  99.9  45.5
## 2 500        100      0  12     59.0  57.1  99.9  43.5
## 3 5000       100      0  23.0   82.9  79.5  99.8  23.2

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(pop_fit_max ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_fit_max by Interval
## Kruskal-Wallis chi-squared = 50.052, df = 2, p-value = 1.353e-11

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$pop_fit_max, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'g')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$pop_fit_max and performance$Interval 
## 
##      50      500    
## 500  1       -      
## 5000 2.6e-09 7.4e-10
## 
## P value adjustment method: bonferroni

5.4.2 Activation gene coverage

Activation gene coverage analysis.

5.4.2.1 Coverage over time

Activation gene coverage over time.

# data for lines and shading on plots
lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_act_cov),
    mean = mean(pop_act_cov),
    max = max(pop_act_cov)
  )

## `summarise()` has grouped output by 'Interval'. You can override using the
## `.groups` argument.

ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 1.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Activation gene coverage over time')+
  p_theme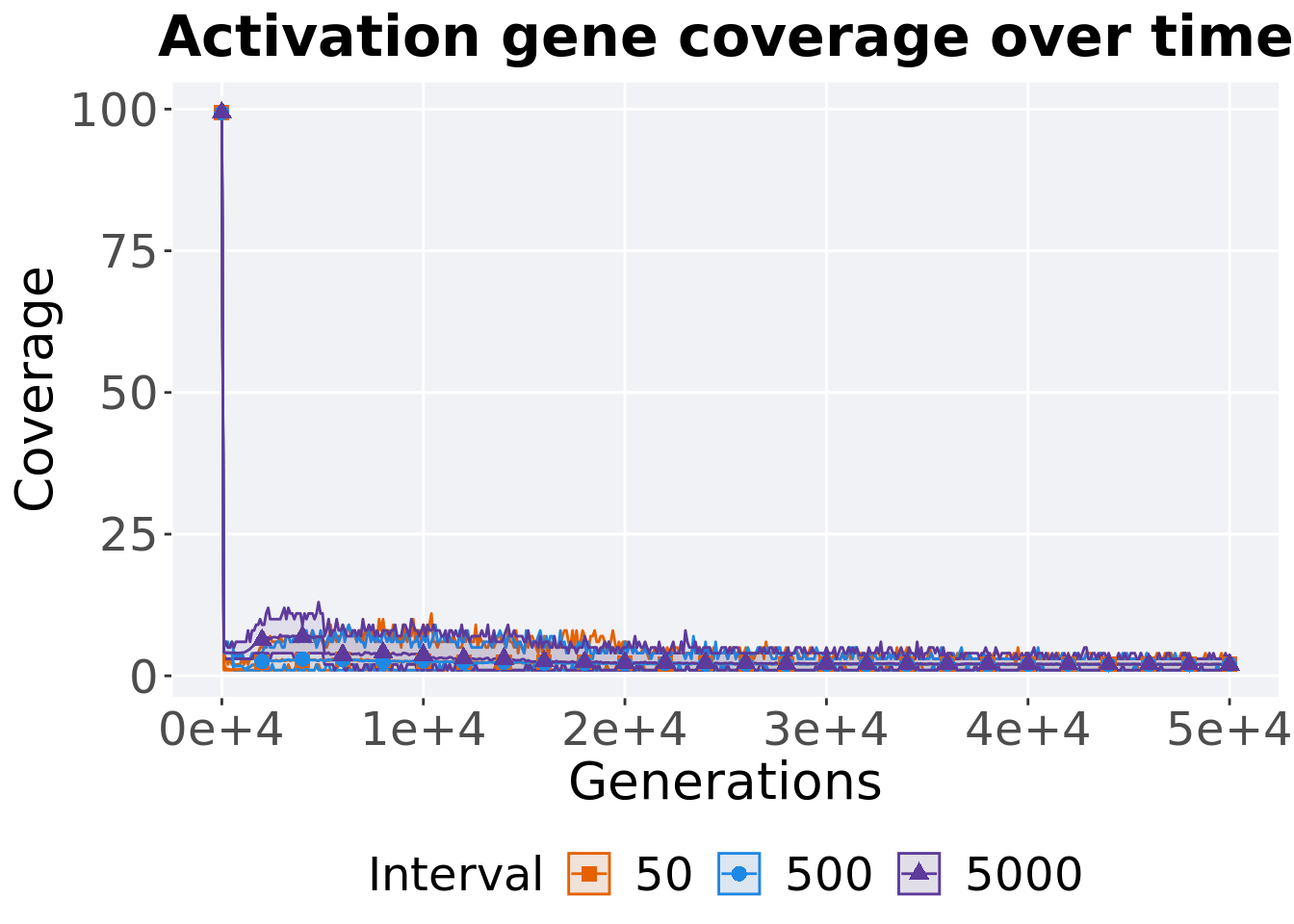

5.4.2.2 End of 50,000 generations

Activation gene coverage in the population at the end of 50,000 generations.

### end of run
filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_act_cov, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.3) +
  geom_point(position = position_jitter(height = .05, width = .05), size = 1.5, alpha = 0.5) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_shape_manual(values=SHAPE)+
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_discrete(
    name="Interval"
  ) +
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final activation gene coverage')+
  p_theme + coord_flip()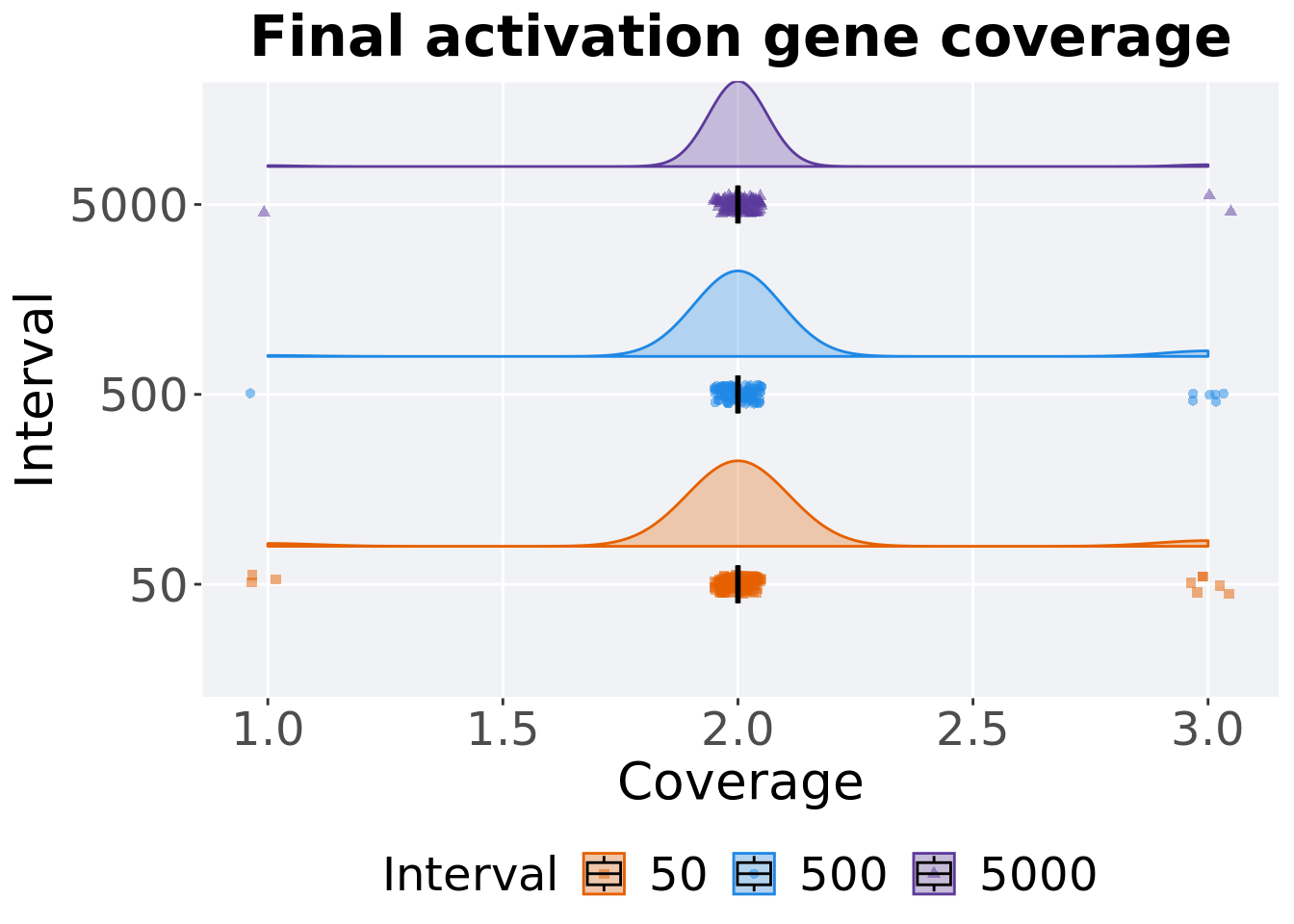

5.4.2.2.1 Stats

Summary statistics for activation gene coverage.

coverage = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'TOURNAMENT' & Generations == 50000)
coverage %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_act_cov)),
    min = min(pop_act_cov, na.rm = TRUE),
    median = median(pop_act_cov, na.rm = TRUE),
    mean = mean(pop_act_cov, na.rm = TRUE),
    max = max(pop_act_cov, na.rm = TRUE),
    IQR = IQR(pop_act_cov, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <int>  <dbl> <dbl> <int> <dbl>
## 1 50         100      0     1      2  2.03     3     0
## 2 500        100      0     1      2  2.05     3     0
## 3 5000       100      0     1      2  2.01     3     0

Kruskal–Wallis test provides evidence of no difference among activation gene coverage.

kruskal.test(pop_act_cov ~ Interval, data = coverage)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_act_cov by Interval
## Kruskal-Wallis chi-squared = 1.299, df = 2, p-value = 0.5223

5.5 Lexicase selection

Here we analyze how the different population structures affect standard lexicase selection on the contradictory objectives diagnostic.

5.5.1 Performance

5.5.1.1 Performance over time

lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_fit_max) / DIMENSIONALITY,
    mean = mean(pop_fit_max) / DIMENSIONALITY,
    max = max(pop_fit_max) / DIMENSIONALITY
  )
ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 2.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle("Performance over time") +
  p_theme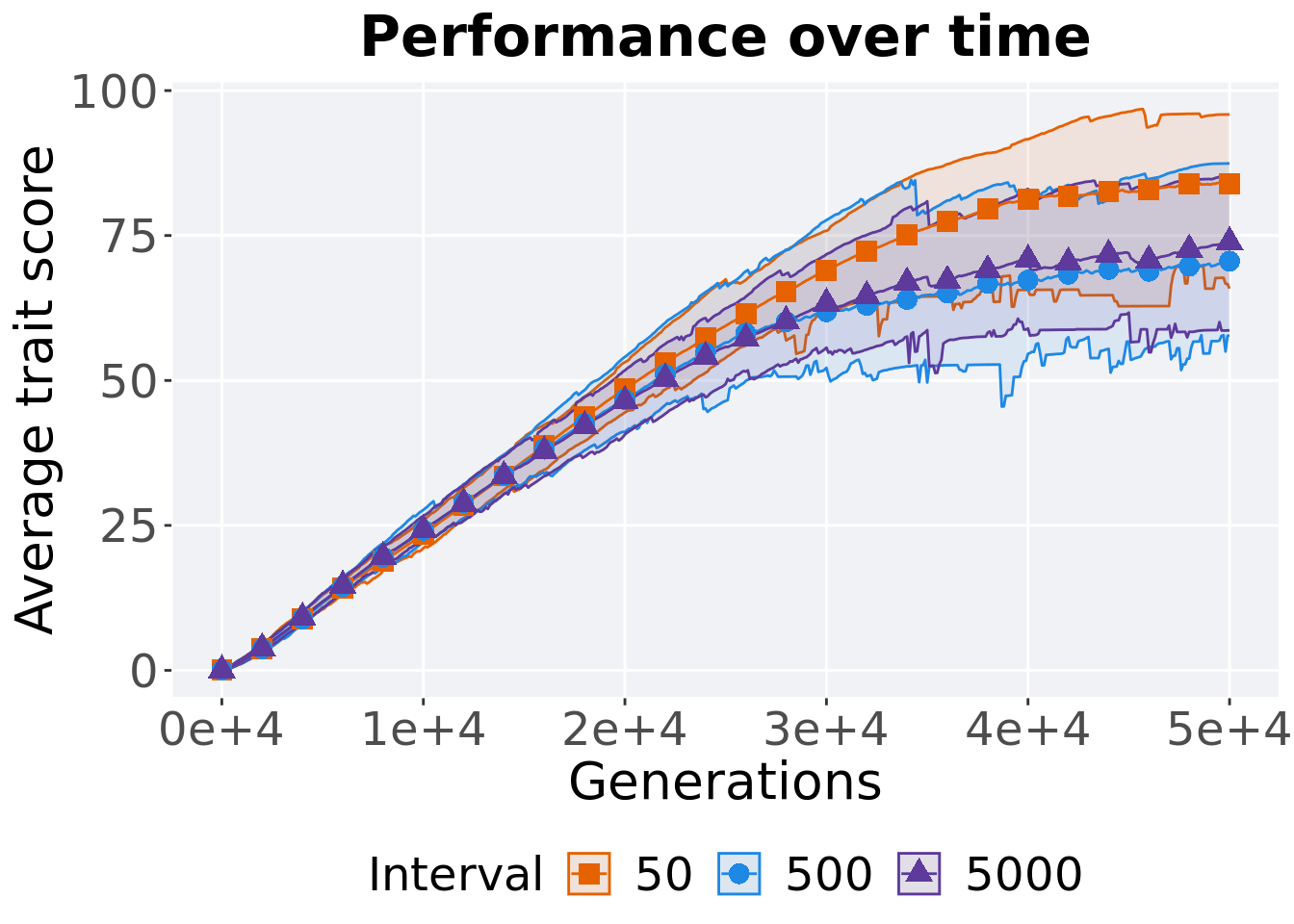

5.5.1.2 Best performance

Best performance is found throughout in final generation.

filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & VAR == 'pop_fit_max') %>%
  ggplot(., aes(x = Interval, y = VAL / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Best performance')+
  p_theme + coord_flip()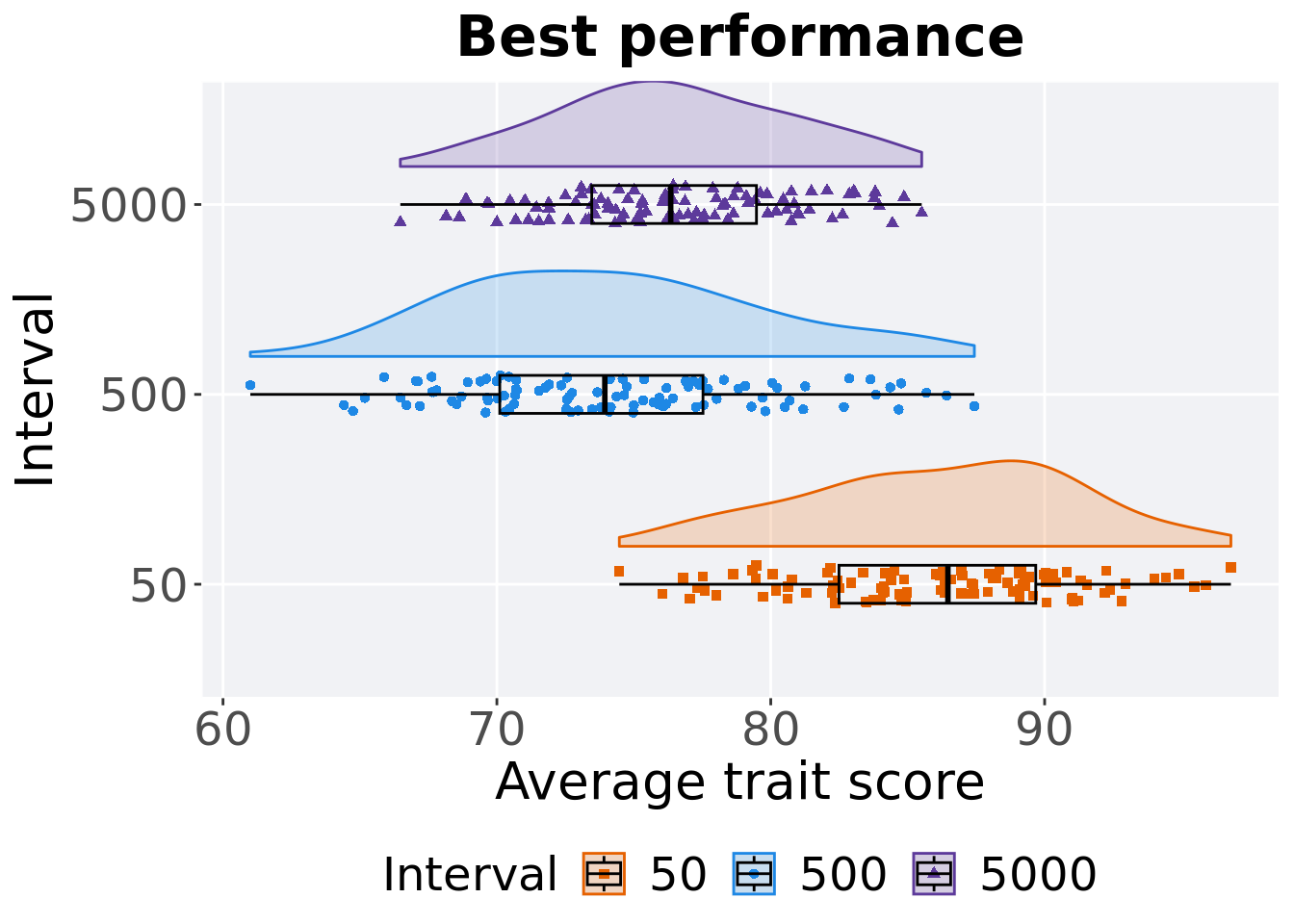

5.5.1.2.1 Stats

Summary statistics for the best performance found.

performance = filter(df_best, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & VAR == 'pop_fit_max')
performance$Interval = factor(performance$Interval, levels = c('50','5000','500'))
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(VAL)),
    min = min(VAL, na.rm = TRUE) / DIMENSIONALITY,
    median = median(VAL, na.rm = TRUE) / DIMENSIONALITY,
    mean = mean(VAL, na.rm = TRUE) / DIMENSIONALITY,
    max = max(VAL, na.rm = TRUE) / DIMENSIONALITY,
    IQR = IQR(VAL, na.rm = TRUE) / DIMENSIONALITY
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0  74.5   86.5  86.1  96.8  7.18
## 2 5000       100      0  66.5   76.3  76.4  85.5  6.01
## 3 500        100      0  61.0   73.9  74.1  87.4  7.42

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(VAL ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  VAL by Interval
## Kruskal-Wallis chi-squared = 155.15, df = 2, p-value < 2.2e-16

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$VAL, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'l')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$VAL and performance$Interval 
## 
##      50     5000  
## 5000 <2e-16 -     
## 500  <2e-16 0.0013
## 
## P value adjustment method: bonferroni

5.5.1.3 Final performance

Best performance is found throughout in final generation.

filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_fit_max / DIMENSIONALITY, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.2) +
  geom_point(position = position_jitter(width = .1), size = 1.5, alpha = 1.0) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_y_continuous(
    name="Average trait score"
  ) +
  scale_x_discrete(
    name="Interval"
  )+
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi, ) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final performance')+
  p_theme + coord_flip()

5.5.1.3.1 Stats

Summary statistics for the best performance is found throughout in final generation..

performance = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & Generations == 50000)
performance$Interval = factor(performance$Interval, levels = c('50','5000','500'))
performance %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_fit_max)),
    min = min(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    median = median(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    mean = mean(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    max = max(pop_fit_max / DIMENSIONALITY, na.rm = TRUE),
    IQR = IQR(pop_fit_max / DIMENSIONALITY, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <dbl>  <dbl> <dbl> <dbl> <dbl>
## 1 50         100      0  65.8   84.4  83.9  95.9  8.35
## 2 5000       100      0  58.6   73.4  73.9  85.5  6.47
## 3 500        100      0  57.7   69.5  70.6  87.4  8.30

Kruskal–Wallis test provides evidence of difference among selection schemes.

kruskal.test(pop_fit_max ~ Interval, data = performance)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_fit_max by Interval
## Kruskal-Wallis chi-squared = 140.97, df = 2, p-value < 2.2e-16

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction.

pairwise.wilcox.test(x = performance$pop_fit_max, g = performance$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'l')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  performance$pop_fit_max and performance$Interval 
## 
##      50      5000   
## 5000 < 2e-16 -      
## 500  < 2e-16 3.8e-05
## 
## P value adjustment method: bonferroni

5.5.2 Activation gene coverage

Activation gene coverage analysis.

5.5.2.1 Coverage over time

Activation gene coverage over time.

# data for lines and shading on plots
lines = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE') %>%
  group_by(Interval, Generations) %>%
  dplyr::summarise(
    min = min(pop_act_cov),
    mean = mean(pop_act_cov),
    max = max(pop_act_cov)
  )

## `summarise()` has grouped output by 'Interval'. You can override using the
## `.groups` argument.

ggplot(lines, aes(x=Generations, y=mean, group = Interval, fill = Interval, color = Interval, shape = Interval)) +
  geom_ribbon(aes(ymin = min, ymax = max), alpha = 0.1) +
  geom_line(size = 0.5) +
  geom_point(data = filter(lines, Generations %% 2000 == 0), size = 1.5, stroke = 2.0, alpha = 1.0) +
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_continuous(
    name="Generations",
    limits=c(0, 50000),
    breaks=c(0, 10000, 20000, 30000, 40000, 50000),
    labels=c("0e+4", "1e+4", "2e+4", "3e+4", "4e+4", "5e+4")

  ) +
  scale_shape_manual(values=SHAPE)+
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Activation gene coverage over time')+
  p_theme

5.5.2.2 End of 50,000 generations

Activation gene coverage in the population at the end of 50,000 generations.

### end of run
filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & Generations == 50000) %>%
  ggplot(., aes(x = Interval, y = pop_act_cov, color = Interval, fill = Interval, shape = Interval)) +
  geom_flat_violin(position = position_nudge(x = .2, y = 0), scale = 'width', alpha = 0.3) +
  geom_point(position = position_jitter(height = .05, width = .05), size = 1.5, alpha = 0.5) +
  geom_boxplot(color = 'black', width = .2, outlier.shape = NA, alpha = 0.0) +
  scale_shape_manual(values=SHAPE)+
  scale_y_continuous(
    name="Coverage"
  ) +
  scale_x_discrete(
    name="Interval"
  ) +
  scale_colour_manual(values = cb_palette_mi) +
  scale_fill_manual(values = cb_palette_mi) +
  ggtitle('Final activation gene coverage')+
  p_theme + coord_flip()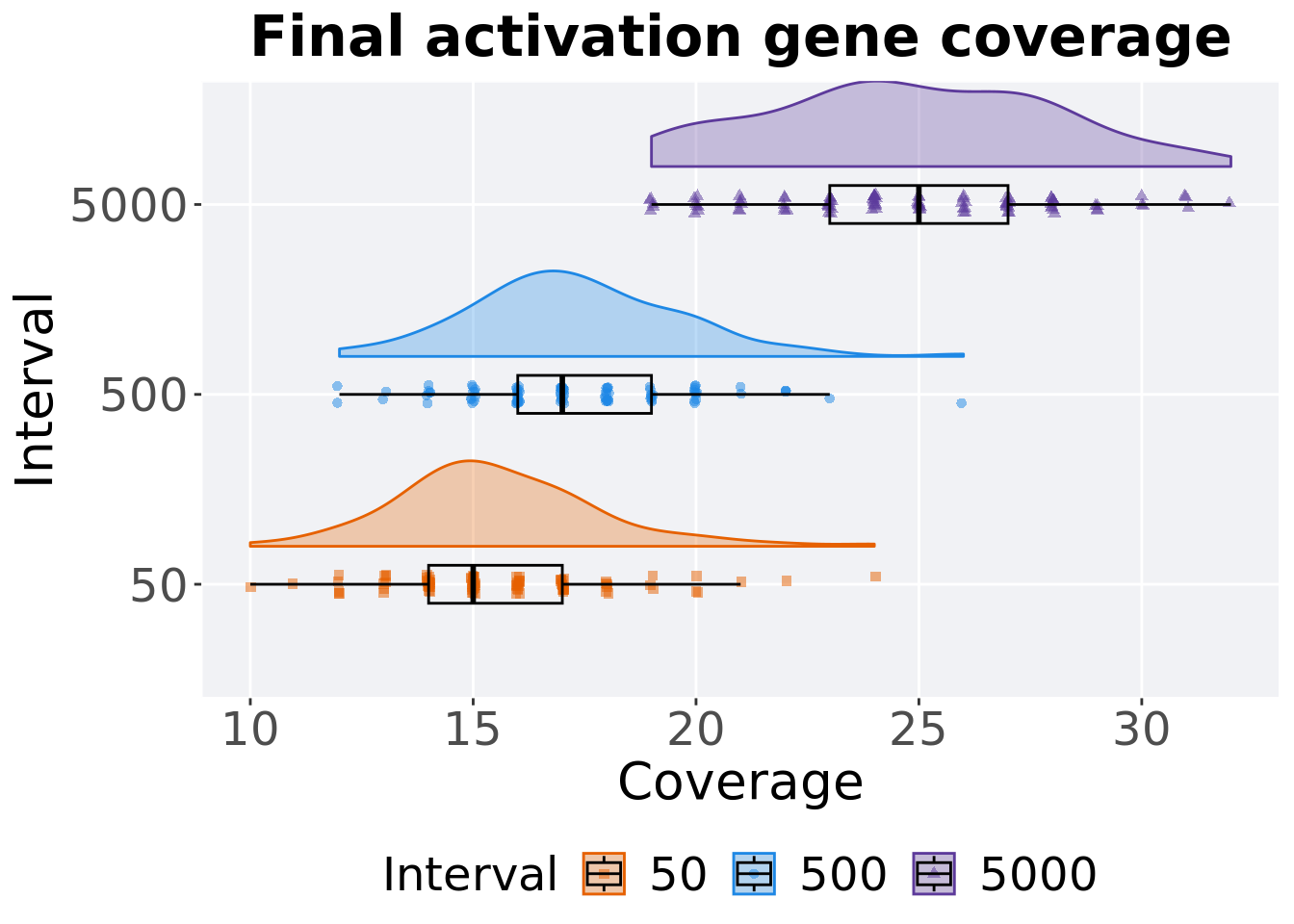

5.5.2.2.1 Stats

Summary statistics for activation gene coverage.

coverage = filter(df_ot, Diagnostic == 'MULTIPATH_EXPLORATION' & `Selection\nScheme` == 'LEXICASE' & Generations == 50000)
coverage$Interval = factor(coverage$Interval, levels = c('50','500','5000'))
coverage %>%
  group_by(Interval) %>%
  dplyr::summarise(
    count = n(),
    na_cnt = sum(is.na(pop_act_cov)),
    min = min(pop_act_cov, na.rm = TRUE),
    median = median(pop_act_cov, na.rm = TRUE),
    mean = mean(pop_act_cov, na.rm = TRUE),
    max = max(pop_act_cov, na.rm = TRUE),
    IQR = IQR(pop_act_cov, na.rm = TRUE)
  )

## # A tibble: 3 x 8
##   Interval count na_cnt   min median  mean   max   IQR
##   <fct>    <int>  <int> <int>  <dbl> <dbl> <int> <dbl>
## 1 50         100      0    10     15  15.6    24     3
## 2 500        100      0    12     17  17.3    26     3
## 3 5000       100      0    19     25  24.8    32     4

Kruskal–Wallis test provides evidence of difference among activation gene coverage.

kruskal.test(pop_act_cov ~ Interval, data = coverage)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  pop_act_cov by Interval
## Kruskal-Wallis chi-squared = 198.08, df = 2, p-value < 2.2e-16

Results for post-hoc Wilcoxon rank-sum test with a Bonferroni correction on activation gene coverage.

pairwise.wilcox.test(x = coverage$pop_act_cov, g = coverage$Interval, p.adjust.method = "bonferroni",
                     paired = FALSE, conf.int = FALSE, alternative = 'g')

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  coverage$pop_act_cov and coverage$Interval 
## 
##      50      500    
## 500  1.3e-07 -      
## 5000 < 2e-16 < 2e-16
## 
## P value adjustment method: bonferroni